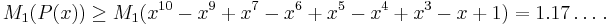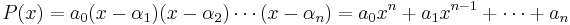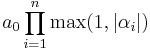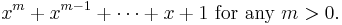Lehmer's conjecture

For Lehmer's conjecture about the non-vanishing of τ(n), see Ramanjuan's tau function.

Lehmer's conjecture, also known as the Lehmer's Mahler measure problem, is a problem in number theory. Derrick Henry Lehmer conjectured that the Mahler measure of any integral polynomial

P(x),

that is not a multiple of cyclotomic polynomials, is bounded below.

More specifically

M_1(P(x))\geq M_1(x^{10}-x^9%2Bx^7-x^6%2Bx^5-x^4%2Bx^3-x%2B1)=1.17\dots\,.

Essentially, to disprove this conjecture, one would try to find a polynomial

P(x)=a_0 (x-\alpha_1)(x-\alpha_2)\cdots(x-\alpha_n)=a_0 x^n%2Ba_1 x^{n-1}%2B\cdots%2Ba_n

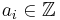with a_i \in \mathbb{Z} (each coefficient is an integer), such that

a_0 \prod_{i=1}^{n} \max(1,|\alpha_i|)

is minimized, and where 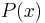P(x) is not divisible by

x^m%2Bx^{m-1}%2B\cdots%2Bx%2B1\text{ for any }m>0.

This can also be stated in terms of the Mahler measure of an algebraic number, where the Mahler measure of an algebraic number is simply the Mahler measure of its minimal polynomial.

Some active research consists of computational techniques for searching through polynomials of some degree trying to find those with smallest Mahler measure.

External links